AVL Tree is often asked in interviews or coding rounds by some companies like Oracle and SAP.Though some people leave AVL trees thinking its not important,but you can never know what they might ask you in interview.So Its good to know about it.If not completely then at least some basic concepts.
AVL Trees are Height Balanced binary search tree datastructure such that for every internal nodes the heights of the two child node differ by at most one.If the balanced is disturbed at any time re-balancing is to be done to again make it balanced.In AVL Tree searching,Insertion and Deletion takes O(logn) time.Insertion and Deletion may require to re-balance the tree using Tree rotation .
Insertion : It is necessary to check the balancing of the tree after insertion of new node.There is a term called balance factor which is calculated as H(left subtree)-H(Right subtree).For each node if the balanced factor remains +1,0 or -1 then there is no need of rotation but if balance factor is less then -1 or greater then +1 then Tree rotation is to be done to restore the balance.If insertion are performed serially after each insertion then atleat one of the cases out of four cases needs to be resolved to restore the balance.
The Four cases are :
Let P be the root node of some tree and R and L be right and left child respectively
If the balance factor of P is -2 then the right subtree outweighs the left subtree of the given node, and the balance factor of the right child (R) must be checked. The left rotation with P as the root is necessary.
Right-Right
If the balance factor of R is -1 , a single left rotation with P as the root is needed which is Right-Right case.
Right-left
If the balance factor of R is +1, two different rotations are needed. The first rotation is a right rotation with R as the root. The second is a left rotation with P as the root which is Right-Left case
If the balance factor of P is 2, then the left subtree outweighs the right subtree of the given node, and the balance factor of the left child (L) must be checked. The right rotation with P as the root is necessary.
Left-Left
If the balance factor of L is +1 , a single right rotation with P as the root is needed which is Left-Left case.
Left-Right
If the balance factor of L is -1, two different rotations are needed. The first rotation is a left rotation with L as the root. The second is a right rotation with P as the root which is Left-Right case.
AVL Trees are Height Balanced binary search tree datastructure such that for every internal nodes the heights of the two child node differ by at most one.If the balanced is disturbed at any time re-balancing is to be done to again make it balanced.In AVL Tree searching,Insertion and Deletion takes O(logn) time.Insertion and Deletion may require to re-balance the tree using Tree rotation .
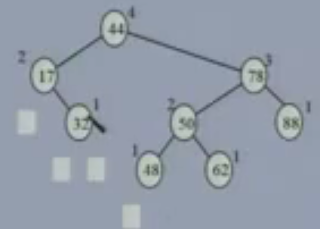
Let the height of last nodes be 1 the node above it be 2 and finally the root node be 4.You can see that the tree is balanced as the height of child nodes of internal nodes differ by the value of 1 or 0.Next we will discuss the Insertion of AVL Tree.
Insertion : It is necessary to check the balancing of the tree after insertion of new node.There is a term called balance factor which is calculated as H(left subtree)-H(Right subtree).For each node if the balanced factor remains +1,0 or -1 then there is no need of rotation but if balance factor is less then -1 or greater then +1 then Tree rotation is to be done to restore the balance.If insertion are performed serially after each insertion then atleat one of the cases out of four cases needs to be resolved to restore the balance.
The Four cases are :
Let P be the root node of some tree and R and L be right and left child respectively
If the balance factor of P is -2 then the right subtree outweighs the left subtree of the given node, and the balance factor of the right child (R) must be checked. The left rotation with P as the root is necessary.
Right-Right
If the balance factor of R is -1 , a single left rotation with P as the root is needed which is Right-Right case.
Right-left
If the balance factor of R is +1, two different rotations are needed. The first rotation is a right rotation with R as the root. The second is a left rotation with P as the root which is Right-Left case
If the balance factor of P is 2, then the left subtree outweighs the right subtree of the given node, and the balance factor of the left child (L) must be checked. The right rotation with P as the root is necessary.
Left-Left
If the balance factor of L is +1 , a single right rotation with P as the root is needed which is Left-Left case.
Left-Right
If the balance factor of L is -1, two different rotations are needed. The first rotation is a left rotation with L as the root. The second is a right rotation with P as the root which is Left-Right case.
Comments
Post a Comment